James Lovelock's Daisyworld
Material zum Themenbereich
,,Komplexe Systeme im Physikunterricht''
von Rolf Carstensen
Institut für die Pädagogik der Naturwissenschaften,
Universität Kiel
Aug 31, 2001
Inhalt
 1 Worum geht es?
1 Worum geht es?
2 Das Gaia-Prinzip und die Daisyworld
3 Das Daisyworld-Modell
4 Experimente mit der Daisyworld
Literaturverzeichnis
Nützliche Links
Download Area
Simulationen der Daisyworld
Inhalt
1 Worum geht es?
Im Physikunterricht beschäftigt man sich häufig mit vielen Einzelphänomenen, wie etwa dem freien Fall oder der
Kondensatorentladung. Es mag dabei der Eindruck entstehen, dass die dabei gefundenen Gesetze im wesentlichen auch
nur geeignet sind ebendiese Phänomene zu beschreiben, nicht aber komplexere Dinge, wie zum Beispiel unser Klimasystem.
Und dieser Einwand ist auch insofern gerechtfertigt, als dass zum Beispiel das Verständnis des Klimasystems einen
weitreichenden interdisziplinären Ansatz erfordert. Moderne Physik beschäftigt sich jedoch mit komplexen Systemen,
insbesondere unter dem Aspekt der nichtlinearen Dynamik.
Das hier vorgestellte Daisyworld-Modell ist ein verhältnismäßig einfaches komplexes System. Es verdeutlicht, wie
man durch eine Betrachtungsweise von außen, dem Denken in Bilanzen und der Ausnutzung von elementaren physikalischen
Gesetzen aber auch von Erkenntnissen aus anderen Disziplinen relativ schnell zu einer adäquaten Beschreibung
des Systemverhaltens kommt. Außerdem zeigt die Daisyworld einige typische Aspekte nichtlinearer Systeme, etwa die
Abhängigkeit der stationären Zustände von dem Anfangszustand des Systems und dem damit verbundenen Gedächtnis,
welches sich nach außen als Hysterese zeigt.
Für das Verständnis der Daisyworld auf der Ebene der Modellierung ist es allerdings erforderlich, dass eine gewisse
Vertrautheit mit Differentialgleichungen vorhanden ist. Dabei kommt es nicht so sehr darauf an, Lösungsstrategien für
Differentialgleichungen zu kennen, sondern vielmehr darauf, deren Bedeutung als Bestimmungsgleichung für Funktionen
verstanden zu haben, also insbesondere, dass Differentialgleichungen die Zeitentwicklung von physikalischen Größen
festlegen, wie zum Beispiel die der Spannung bei der Kondensatorentladung.
Aus diesen Gründen ist die Daisyworld eher für Schüler aus den höheren Jahrgängen der gymnasialen Oberstufe
geeignet. Ebenfalls wäre es günstig, wenn die Schüler sich überhaupt schon mal mit der Modellierung von
physikalischen Systemen beschäftigt haben. Viel Material dazu und auch eine kurze Abhandlung über das numerische Lösen
von Differentialgleichungen bietet das Buch von Horst P. Schecker[3].
Inhalt
2 Das Gaia-Prinzip und die Daisyworld
Um einen tiefgehenden Einblick in die Gaia-Hypothese zu erhalten, lohnt es sich, das Buch von
James Lovelock [1] zu lesen, zumal es recht witzig geschrieben ist. Es behandelt allerdings nicht die
mathematischen Aspekte des Modells. Im folgenden werden wir das Gaia-Prinzip in aller Kürze kennenlernen und einen
Einblick in die Daisyworld auf anschaulicher Ebene gewinnen.
Das Gaia-Prinzip
Es ist die Philosophie des Gaia-Prinzips, die Erde in ihrer Gesamtheit als Lebewesen zu betrachten. Daraus ergibt sich
der Forschungsansatz, ebendieses Gesamtsystem an sich zu untersuchen und nicht die diversen Teilsysteme. Es ist ein
interdisziplinärer Ansatz, bei dem davon ausgegangen wird, dass sich nicht nur die einzelnen Lebewesen ihrer Umwelt
anpassen und diese sich im wesentlichen unabhängig entwickelt, sondern dass in Wahrheit ein kompliziertes Verbund-
und Rückkopplungssystem vorliegt. Das heißt, dass die Lebewesen sich sowohl an ihre Umwelt anpassen, als auch, dass
die Umwelt sich in einer Art Koevolution an die Lebewesen anpasst und damit wiederum auf deren Entwicklung
zurückwirkt.
Es ist mittlerweile recht eindeutig, dass solche Rückkopplungssysteme tatsächlich dafür verantwortlich sind, dass
viele Größen, die unsere Umgebung charakterisieren, konstant bleiben, wie zum Beispiel die mittlere globale
Temperatur und der CO2-Gehalt. In Anlehnung an die Physiologie von Lebewesen wird dieses Verhalten als
Homöostasis (wie zum Beispiel das Konstanthalten der Körpertemperatur) bezeichnet.
Das Gaia-Prinzip wurde häufig als teleologische Weltsicht kritisiert, da es zuweilen dahingehend fehlinterpretiert
wurde, dass es den Lebewesen auf irgendeine Weise innewohnt, wie sie sich zu entwickeln haben, damit die dadurch
gebildete Umwelt für das Gesamtsystem einen günstigen Lebensraum darstellt. Denn woher sollen die einzelnen Lebewesen
das wissen? Um zu zeigen, dass den Lebewesen keineswegs eine solche Zielgerichtheit eingeimpft sein muss, sondern die
Entwicklung von Lebewesen und Umwelt schlichtweg durch die gegenseitigen Abhängigkeiten erzwungen wird, hat James
Lovelock die Daisyworld erschaffen, ein Modell, das man sozusagen schon als Karikatur unseres Planeten bezeichnen
könnte und das die wesentlichen Prinzipien der Gaia-Hypothese veranschaulicht.
Die Daisyworld
Die Daisyworld ist ein imaginärer Planet ähnlich der Erde, der im einfachsten Fall von genau zwei Sorten von Pflanzen
bewachsen ist, nämlich von schwarzen und weißen Gänseblümchen (Daisies). Diese Blümchen wachsen bei Temperaturen
zwischen 5° C und 40°C
mit einem Optimum bei etwa 22°C und müssen miteinander
um den Platz konkurrieren. Wasserflächen sind auf diesem Planeten vernachlässigbar klein, allerdings ist dennoch für
eine ausreichende Versorgung der Pflanzen mit Wasser gesorgt.
Energie bezieht der Planet einzig und allein von seiner Sonne. Je nach Beschaffenheit seiner Oberfläche -
genaugenommen deren Albedo - wird ein Teil dieser Energie unmittelbar wieder reflektiert. Um nicht zu überhitzen,
strahlt der Planet die restliche Energie durch Wärmestrahlung ab und zwar in Abhängigkeit von seiner Temperatur, wie
es das Stefan-Boltzmannsche Strahlungsgesetz besagt.
Der Energiefluss von der Sonne ist nun nicht zu allen Zeiten konstant, sondern nimmt mit der Zeit zu. Dies liegt
daran, dass bei den Fusionsprozessen im Inneren der Sonne Helium entsteht. Diese Helium verschiebt das bestehende
Gleichgewicht zwischen thermischem Druck (wirkt nach außen) und Gravitationsdruck (wirkt nach innen) derart, dass sich
der Stern ausdehnt, also größer wird und stärker strahlt. Der Daisyworld gelingt es dennoch, ihre Temperatur über
einen weiten Bereich annähernd konstant zu halten und zwar aus folgendem Grund: In Zeiten geringerer Einstrahlung
haben die schwarzen Gänseblümchen eine höhere lokale Temperatur als die weißen Gänseblümchen, da sie mehr
Sonnenlicht absorbieren. Dadurch haben sie, sofern die Temperatur noch nicht zu heiß ist, einen Wachstumsvorteil
gegenüber den weißen Gänseblümchen, so dass der ganze Planet eher von schwarzen Gänseblümchen bevölkert wird als
von weißen, was zu einer Anhebung der Temperatur auf dem ganzen Planeten führt. Sollte die solare Einstrahlung jetzt
aber zunehmen, so würde es nur mit schwarzen Gänseblümchen zu heiß werden. Jetzt bekommen die weißen
Gänseblümchen einen Wachstumsvorteil und treten an die Stellen der schwarzen Gänseblümchen. Der ganze Planet wird
also allmählich eher weiß, was durch die höhere Reflektion eine Kühlung bewirkt. Insgesamt verhält sich das System
so, dass sich eine Temperatur von etwa 22° C einstellt, also beim Optimum des Pflanzenwachstums. Es liegt
also ein natürliches Regelsystem vor, bedingt durch die negative Rückkopplung über die sich verändernde Albedo.
Wenn man die Solarkonstante mit der Zeit von 60% auf 140% des heutigen Wertes erhöht, ergibt sich das Bild aus
Abbildung 1.
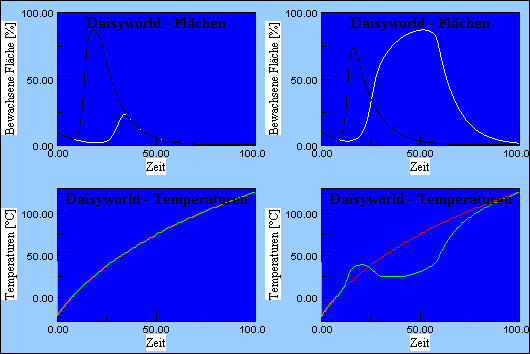
Abbildung 1: Entwicklung der Temperatur und der Pflanzen bei Erhöhung der Solarkonstanten.
Links: Ohne Rückkopplung durch die Albedo. Rechts: Mit Rückkopplung durch die Albedo.
Offensichtlich sorgt die Rückkopplung über die Albedo dafür, dass die Pflanzen für einen weiten Bereich in der Lage
sind, die Temperatur zu stabilisieren.
Die Temperatur auf der Daisyworld steht stellvertretend für ihr gesamtes Klima. In der Realität ist Klima natürlich
vielschichtiger und entsprechend schwierig zu modellieren. Hinter dem einfachen Daisyworld-Modell verbirgt sich
aber ein allgemeines Regelprinzip, welches im englischen Sprachraum als ''integral rein control'' bezeichnet wird und
welches unser Körper zum Beispiel zur Regulierung des Blutzuckerspiegels verwendet, siehe Daisyworld & beyond.
Inhalt
3 Das Daisyworld-Modell
In diesem Abschnitt soll das mathematische Modell erläutert werden, welches die Daisyworld beschreibt. Die
Grundgleichungen stammen im wesentlichen aus dem Bereich der Physik, aber auch aus der Biologie und insbesondere der
theoretischen Ökologie.
Zeitentwicklungsgleichungen
Die schwarzen und die weißen Gänseblümchen müssen also um den Platz auf dem Planeten konkurrieren - die eine
Sorte kann sich nur soweit ausbreiten, wie die andere ihr noch freie Fläche dazu übriglässt. Zur Beschreibung
der jeweiligen Population eignet sich als Modellgröße die von der jeweiligen Sorte bewachsene Fläche, wir werden
die Flächen mit Aw für die weißen, Ab für die schwarzen (b: black) und Ag für den unbedeckten Grund
bezeichnen. Die Gesamtfläche des Planeten setzen wir willkürlich zu 1 beziehungsweise 100% , so dass die drei
Flächen alle Werte zwischen 0 und 1 annehmen. Das Weglassen von Einheiten ist in der Computernumerik üblich, da
ein Computer von sich aus ohnehin nur mit Zahlen rechnet.
Als Wachstumsmodell könnte man sich vorläufig zunächst einmal gewöhnliches exponentielles Wachstum vorstellen,
also zum Beispiel für die weißen Gänseblümchen eine Differentialgleichung der Form
mit einer geeigneten Geburtenrate b und der bekannten Lösung
Dies würde aber bedeuten, dass die weißen Gänseblümchen bis ins
Unermessliche wachsen, von Konkurrenzdruck keine Spur. Deswegen ist es sinnvoll die Geburtenrate abhängig von der noch
unbewachsenen Fläche Ag zu machen, im einfachsten Fall proportional dazu. Wir schreiben also für die weißen
Blümchen
Es ist jetzt bw Ag die Geburtenrate, so dass wir den Faktor
bw alleine als Wachstumsfaktor bezeichnen wollen. Über diesen Faktor soll später die
Temperaturabhängigkeit eingebracht werden und die Temperaturen werden für weiße Gänseblümchen anders sein als
für die schwarzen, daher der Index w.
Natürlicherweise sterben auch immer mal ein paar Pflanzen, so dass es sinnvoll ist
eine Sterberate c einzuführen. Die Gleichung für die schwarzen Gänseblümchen sieht
- mal abgesehen - von den Indizes ganz genauso aus wie die für die weißen, so dass die gesamte Zeitentwicklung durch folgende
Gleichungen beschrieben werden kann:
Die letzte Gleichung berücksichtigt dabei die oben geforderte Rahmenbedingung, dass die Gesamtfläche des Planeten 1
beträgt.
Betrachten wir jetzt dieses Differentialgleichungssystem noch einmal genauer. Was hat sich gegenüber unserer
Ausgangsgleichung für exponentielles Wachstum geändert? Die Ausgangsgleichung ist eine lineare Differentialgleichung,
das heißt die Funktion Aw und ihre Ableitung gehen nur in der 1. Potenz in die Gleichung ein. Das
Differentialgleichungssystem ist hingegen nicht mehr linear, was man erkennt, wenn man zum Beispiel die dritte
Gleichung in die erste einsetzt. Die Funktion Aw geht dann quadratisch ein und außerdem taucht der (nichtlineare)
gemischte Term Aw Ab auf. Die Tatsache, dass Nichtlinearität vorliegt, hat weitreichende Konsequenzen, wie wir
noch sehen werden, zum Beispiel was die Eindeutigkeit von Lösungen betrifft.
Solche oder ähnliche Gleichungen werden in der theoretischen Ökologie eingesetzt.
Temperaturabhängiges Wachstum
Unsere Gänseblümchen sollen zwischen 5° C und 40° C
wachsen mit einer optimalen Temperatur für das Wachstum bei etwa 22° C. Der Wachstumsfaktor
soll über den gesamten Wachstumsbereich durch eine Parabel angenähert werden,
siehe Abbildung 2.
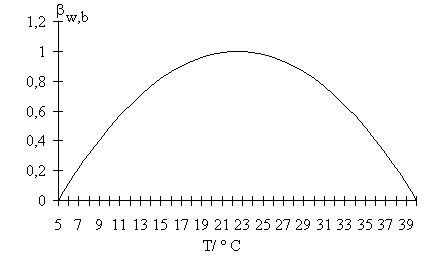
Abbildung 2: Temperaturabhängiges Wachstum der Pflanzen. Wachstum ist möglich bei Temperaturen
zwischen 5° C und 40° C,
mit einem Optimum bei etwa 22°C
Der Wachstumsfaktor wird dabei ohne Einheit auf Werte zwischen 0 und 1 beschränkt. Außerhalb des dargestellten
Bereichs ist er konstant 0. Aus der Biologie weiß man, dass das Pflanzenwachstum tatsächlich eine in etwa
parabelförmige Temperaturabhängigkeit zeigt.
Einstellung der planetaren Temperatur durch ein dynamisches Gleichgewicht
Genau wie jeder Planet kann die Daisyworld ihre Temperatur nur dann halten, wenn sie genau so viel Energie pro Zeit
abstrahlt (Paus), wie sie von der Sonne empfängt (Pein).
Diese Bilanzgleichung beschreibt also ein dynamisches Gleichgewicht.
Ein Teil der Leistung, die die Daisyworld von der Sonne in Form von Strahlung erhält, wird sofort wieder reflektiert.
Die Größe dieses Anteils hängt von der planetaren Albedo ap ab, einem
numerischen Wert zwischen 0 und 1, beziehungsweise 0% und 100%. Die planetare Albedo ist das gewichtete Mittel über
die Albedo der einzelnen Flächen (weiße Blümchen: aw, unbedeckter Grund:
ag und schwarze Blümchen: ab), also
Dabei haben die weißen Blümchen natürlich ein höheres Reflexionsvermögen als die schwarzen und der unbedeckte
Grund möge dazwischen liegen:
Wir können nun die Gleichung für die eingestrahlte Intensität aufstellen, das ist der Teil von der
Sonneneinstrahlung, der nicht reflektiert wird:
Die Solarkonstante ist mit S0 = 3668 W/( m2) etwas größer gewählt für die Daisyworld. Vermutlich
wollte James Lovelock, dass die Temperaturen auch ohne Berücksichtigung des Treibhauseffektes in einem
anschaulichen Wertebereich liegen, sprich um die 20° C. Mit L = 0,6 ... 2,4
haben wir einen zusätzlichen Trimmfaktor eingeführt, mit dem wir die Sonneneinstrahlung mit der Zeit verändern können.
Alternativ könnte man natürlich einfach S0 verändern, aber so wissen wir, dass die Sonneneinstrahlung bei einem
Wert von L = 1,0 dem heutigen Wert entspricht.
Für die Daisyworld nehmen wir vereinfacht an, dass sie sich wie ein schwarzer Strahler verhält. Es werden also kein
Treibhauseffekt oder Wolkenbildung berücksichtigt. Die abgestrahlte Intensität berechnet sich dann nach dem
Strahlungsgesetz von Stefan und Boltzmann:
Tp ist die mittlere Temperatur, die ein Beobachter von außerhalb der Daisyworld durch Messung der
Temperaturstrahlung feststellen würde. s = 5,67×10-8 W/( K4 m2)
ist die Stefan-Boltzmann-Konstante. Man beachte, dass diesem Gesetz die Kelvin-Skala zugrunde liegt.
Bei der Ausnutzung der Gleichung für die Leistungsbilanz ist schließlich noch zu berücksichtigen, dass der Planet
die Sonneneinstrahlung nur mit seinem Querschnitt aufnimmt, während die Abstrahlung aufgrund seiner Temperatur über
die gesamte Oberfläche erfolgt, siehe Abbildung 3.
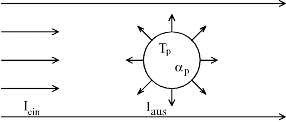
Abbildung 3: Der Planet nimmt mit seinem Querschnitt die von der Sonne eingestrahlte Energie auf, bis auf den Teil,
den er sofort reflektiert. Der restliche Teil wird von der gesamten Oberfläche in Form von
Wärmestrahlung wieder abgegeben.
Es ergibt sich somit:
Den planetaren Radius R braucht man offensichtlich nicht zu kennen, weil er sich herauskürzt. Nach Einsetzen in die
Leistungsbilanzgleichung am Anfang dieses Abschnittes und unter Ausnutzung der Gleichungen für die Intensitäten
erhalten wir:
Lokale Temperaturen und Wärmetransport
In dem letzten Abschnitt haben wir gesehen, dass man mit relativ elementaren physikalischen Gesetzen eine Gleichung
zur Bestimmung der planetaren Temperatur finden kann. Diese könnte man nun natürlich verwenden, um die
Wachstumsfaktoren für die Pflanzen zu bestimmen. Doch was wäre damit erreicht? Die weißen Pflanzen würden sich
exakt genauso wie die schwarzen vermehren, die Wachstumsfaktoren wären ja gleich. Dann gäbe es aber keine
temperaturbedingten Vorteile für die eine oder die andere Sorte. Die Daisyworld soll aber gerade zeigen, dass
Klimaregelung allein durch Ausnutzen von Evolutionsvorteilen möglich ist. Außerdem ist es rein anschaulich klar, dass
die schwarzen Gänseblümchen stets eine etwas höhere Temperatur haben müssen als die weißen, man denke nur an
das Tragen von heller oder dunkler Kleidung im Sommer. Wir führen also für die Pflanzen lokale Temperaturen ein,
Tw für die weißen und Tb für die schwarzen. Wie hängen aber nun diese Temperaturen mit der planetaren
Temperatur Tp zusammen? Die Antwort lautet über Wärmetransport. Wir kommen jetzt in einen Bereich, der sich nicht
mehr so elementar behandeln lässt wie die vorhergehenden Bereiche, da Wärmetransportphänomene schon ein hohes Maß
an physikalischen und mathematischen Kenntnissen voraussetzen. Relativ leicht kann man aber Zugang zu Spezialfällen
finden: Einen Spezialfall haben wir schon kennengelernt, den des unendlich großen Wärmetransports. In dem Fall
würden Temperaturdifferenzen sofort ausgeglichen werden. Demzufolge wären alle Temperaturen gleich, also
Tw = Tp = Tb. Für die weißen Blümchen würde das bedeuten:
Der andere Spezialfall wäre die vollständige Isolation, also kein Wärmetransport.
In diesem Fall wäre es für die weißen Blümchen so, als wenn sie auf einem rein weißen Planeten leben würden und
für die schwarzen entsprechend, als wenn sie auf einem rein schwarzen Planeten leben würden. Die gleiche
Energiebilanzrechnung wie im letzten Abschnitt würde dann für die weißen Blümchen zu der Gleichung
führen. Im Falle eines endlichen, nicht verschwindenden Wärmetransports wird die Temperatur irgendwo zwischen diesen
Extremfällen liegen. Um eine genauere (und aufwändigere) Lösung dieses Problems zu umgehen, welche für das einfache
Daisyworld-Modell auch gar nicht nötig ist, wendet man einen Trick an. Man führt einen sogenannten
Transportparameter R ein, der zwischen den beiden Extremfällen ,,überblendet'':
|
Tw4 = R(1-aw) |
L S0
4 s
|
+(1-R)(1-ap) |
L S0
4 s
|
|
|
Für R = 1 liegt vollständige Isolation vor und für R = 0 vollständiger Wärmetransport. Werte zwischen 0 und 1
stehen dann für den gewünschten endlichen, nicht verschwindenden Wärmetransport.
Die letzte Gleichung lässt sich unter Verwendung der Gleichung für Tp4 noch etwas vereinfachen. Außerdem gilt
für die schwarzen Gänseblümchen natürlich eine entsprechende Gleichung, so dass wir letztlich erhalten:
|
Tw4 = |
R L S0
4 s
|
(ap-aw)+Tp4 |
|
|
Tb4 = |
R L S0
4 s
|
(ap-ab)+Tp4 |
|
Damit ist jetzt die Beschreibung des Modells abgeschlossen. Es soll noch kurz erwähnt werden, dass in der hier
zur Verfügung gestellten Implementation der Daisyworld nicht direkt der Faktor R beeinflusst werden kann, sondern
die Größe 1-R. Dadurch ergibt sich die einfache Assoziation - je größer der Wert, desto größer der
Wärmetransport. Die Gleichungen wurden aber dennoch so aufgestellt, wie sie sind, um Verwirrungen beim Lesen von
Publikationen anderer Autoren zu vermeiden.
Inhalt
4 Experimente mit der Daisyworld
Der große Vorteil des Daisyworld-Modells ist, dass man es auf jedem PC simulieren kann. Die Umsetzung kann auf
verschiedene Weisen geschehen, zum Beispiel mit dem Mathematik-Paket Maple V oder einer Programmiersprache, wobei
man sich im letzten Fall um ein numerisches Verfahren zur Lösung von Differentialgleichungen kümmern muss. Bei dem frei
erhältlichen Programmpaket Easy Java Simulations sind solche Verfahren bereits implementiert, auch muss man sich
wenig um Details der Graphikausgabe kümmern sondern kann die Modellgleichungen praktisch so eingeben, wie sie sind.
Daher sind die nun folgenden Simulationen mit dieser Software geschrieben worden.
Temperaturregelung
Wenn Sie sich jetzt gleich die Simulation anschauen, dann finden Sie auf der linken Seite die Kontrollmöglichkeiten,
wie die Flächenbelegung des Planeten zum Startzeitpunkt und die Größe des Wärmetransports. Auf der rechten Seite
finden Sie Momentanwerte, wie die aktuelle Flächenbelegung und die einzelnen Temperaturen, darunter auch die
Temperatur, wie sie wäre, wenn der Planet gänzlich unbewachsen wäre. Genau diese Größen sind auch in den
Displays in der Mitte graphisch dargestellt, die Zuordnung erfolgt über die Farben. Unten befindet sich ein Regler
für die Sonneneinstrahlung, die in Einheiten des heutigen Wertes eingestellt werden kann. Wenn Sie die Simulation
jetzt starten, wird die Sonneneinstrahlung automatisch mit der Zeit erhöht und es zeigt sich, wie die Daisyworld
auf diesen äußeren Einfluss reagiert. Die Kontrollelemente zur Ablaufsteuerung befinden sich in der oberen Zeile.
,,Start'' startet die Simulation, ,,Stop'' hält sie an, ,,Neustart'' versetzt sie in den Anfangszustand zurück
inklusive aller Parameter, während ,,Löschen'' nur die Zeit zurücksetzt und das Display löscht. ,,Anleitung''
zeigt eine Anleitung, die das Wesentliche aus diesen Abschnitten zusammenfässt.
Simulation laden
Offensichtlich haben die schwarzen Gänseblümchen zu Zeiten geringer Sonneneinstrahlung einen Evolutionsvorteil
gegenüber den weißen, da sie sich selbst zu einer etwas höheren Temperatur verhelfen. Dann kommt ein Bereich, in dem
beide Pflanzensorten gut nebeneinander existieren können, aber mit weiter ansteigender Sonneneinstrahlung setzen
sich die weißen durch, da ihre Farbe ihnen jetzt zum Vorteil wird. Irgendwann ist dann der Punkt erreicht,
wo überhaupt kein Leben mehr möglich ist. Interessant ist allerdings der Temperaturverlauf. Während die Temperatur
eines vergleichbaren unbelebten Planeten kontinuierlich steigt (rote Kurve), so hält die Daisyworld ihre Temperatur
- solange Leben vorhanden ist - doch in einem weiten Bereich in recht gemäßigten Bahnen (grüne Kurve). Wenn man
noch mehr Farbnuancen zulässt außer schwarz und weiß, also 20 verschiedene Pflanzen und mehr, dann verläuft die
Temperaturkurve der Daisyworld extrem glatt in der Höhe der Temperatur für optimales Wachstum bei etwa
22°C, siehe zum Beispiel die Simulation
von Ginger Booth. James Lovelock argumentiert
daher, dass die Erhaltung von Artenreichtum auch unter dem Aspekt der Klimastabilisierung wichtig sein kann. Außerdem
ist es erstaunlich, dass zunehmende Komplexität sich in diesem Fall als stabilisierend auf das System auswirkt. Ein
eher untypisches Verhalten.
Stationäre Zustände
Als Nächstes bietet die Simulation nun die Möglichkeit, zu gegebener Sonneneinstrahlung den Einschwingvorgang
in den stationären Zustand darzustellen. Dazu müssen Sie das Häkchen ,,Automatisch'' rechts unten löschen.
Anschließend kann man links die Startwerte einstellen und unten die Sonneneinstrahlung. Probieren sie zum Beispiel bei
einer Sonneneinstrahlung von 1,2 des heutigen Wertes und einem Wärmetransport von 0,7 nacheinander die Startwerte
10 % Flächenanteil und 90 % Flächenanteil für die weißen Gänseblümchen aus.

Simulation laden
Sie können natürlich auch noch versuchen, in anderen Bereichen stationäre Zustände aufzufinden und dabei ebenfalls
die Größe des Wärmetransports mitzuverändern. Es zeigen sich folgende Dinge: Zunächst einmal benötigt das System
eine gewisse Zeit, um einen stationären Zustand zu erreichen. Genaugenommen findet natürlich eine asymptotische
Annäherung statt, so dass der stationäre Zustand erst im Unendlichen erreicht wird. Wie in solchen Fällen üblich
könnte man aber so etwas wie eine Halbwertszeit einführen. Diese Zeit hätte die Bedeutung einer Relaxationszeit,
also der Zeit, die das System braucht um nach einer Störung wieder in einen Gleichgewichtszustand zu kommen. Dies wird
im nächsten Abschnitt noch einmal wichtig.
Zum anderen existieren bei einer Sonneneinstrahlung von 1,2 offensichtlich mindestens zwei verschiedene stationäre
Zustände, abhängig vom Anfangszustand des Systems. Diese Mehrdeutigkeit der Lösung liegt an der Nichtlinearität
des zugrundeliegenden Differentialgleichungssystem. Im Extremfall können solche Nichtlinearitäten sogar zu
chaotischem Verhalten führen. Dies ist zwar schon seit langer Zeit bekannt; die nichtlineare Dynamik stellt aber
immer noch ein sehr aktuelles Forschungsgebiet dar.
Das Auftreten von mehreren stationären Zuständen im oben geschilderten Fall lässt sich aber auch anschaulich
erklären: Wenn die weißen Blümchen nur mit 10 % Flächenanteil starten, dann ist der Planet bereits so heiß,
dass sie sich auch nicht mehr entwickeln können. Starten sie hingegen mit 90 % Flächenanteil, so können sie
den Planeten soweit vor der Sonneneinstrahlung bewahren, dass sie selbst wachsen können.
Hysterese
In den meisten Simulationen zum Thema ,,Daisyworld'' wird nur der aufsteigende Ast der Temperaturkurve gezeigt, also
die Erhöhung der Sonneneinstrahlung mit der Zeit. Dies entspricht ja auch den tatsächlichen Verhältnissen bei
Sternen wie unserer Sonne. Wie wir aber im letzten Abschnitt gesehen haben, können zu bestimmten Werten auch
verschiedene stationäre Zustände erreicht werden. Das ist notwendige Voraussetzung für das Auftreten von Hysterese
und daher ist es interessant zu gucken, was passiert, wenn man die Sonneneinstrahlung wieder erniedrigt, nachdem sie
ihren (willkürlich festgelegten) Höchststand erreicht hat.
In der nun folgenden Simulation liegt das Augenmerk auf der mittleren planetaren Temperatur (grüne Kurve). Sie wird
über der Sonneneinstrahlung aufgetragen, wobei der Parameter für die Sonneneinstrahlung zunächst langsam stufenweise
erhöht wird und dann wieder erniedrigt. Die Zeit, die zwischen den Stufen gewartet werden muss, muss groß sein
gegenüber der Relaxationszeit, damit das System quasi eine Folge von Gleichgewichtszuständen durchläuft. Im
,,automatischen'' Modus macht die Simulation das selbst (Häkchen ,,Automatisch'' gesetzt). Wenn Sie die
Sonneneinstrahlung lieber selbst erhöhen oder erniedrigen wollen, zum Beispiel um kleinere Bereiche abzufahren, dann
können Sie dies mit den Pfeiltasten des unteren Kontrollbalkens tun. Das Häkchen ,,Automatisch'' muss dazu gelöscht
sein und Sie müssen zwischen den Schritten warten, bis sich die Punkte der Kurve nicht mehr verändern. Zum Vergleich
wird übrigens auch immer die Temperatur des Planeten, wie sie sein würde, wenn er gänzlich unbewachsen wäre,
aufgetragen (rote Kurve). Ansonsten ist die Simulation ganz ähnlich aufgebaut wie die vorige: Rechts werden die
Momentanwerte für Flächen und Temperaturen angezeigt, links kann der Wärmetransport eingestellt werden und oben
befinden sich die Schaltflächen zur Ablaufsteuerung, ergänzt um eine Statusanzeige und ansonsten wie gehabt.
Simulation laden
Sie können auch noch einmal schauen, was passiert, wenn Sie den Kontrollregler für den Wärmetransport in seine
Extrempositionen schieben. In beiden Fällen sollte keine Hysterese auftreten.
Inhalt
Literaturverzeichnis
- [1]
-
J. Lovelock, Das Gaia-Prinzip. Die Biographie unseres Planeten, Insel Taschenbuch
- [2]
-
D. Olbers, P. Lemke, Physik des Klimasystems, Vorlesungsskript, Institut für Meereskunde, Universität Kiel
- [3]
-
H.P. Schecker,Physik - Modellieren,Klett Verlag
- [4]
-
H. Heuser,Gewöhnliche Differentialgleichungen, B. G. Teubner
Inhalt
Nützliche Links
Inhalt
Download Area
- Simulation der Daisyworld:
Die Zip-Datei enthält die eigentliche Simulation als jar-file und zwei
weitere jar-files, die zu Easy Java Simulations gehören und benötigt werden. Außerdem ist eine Batch-Datei
vorhanden, die das Applet startet. Dazu wird JRE (Java Runtime Environment) benötigt. JRE muss von der
Sun-Webseite heruntergeladen werden.
Daisysim1.ZIP (252K)
- Simulation der Hysterese der Daisyworld:
Die Zip-Datei enthält die eigentliche Simulation als jar-file
und ein weiteres jar-file, welches zu Easy Java Simulations gehört und benötigt wird. Außerdem ist eine
Batch-Datei vorhanden, die das Applet startet. Dazu wird JRE (Java Runtime Environment) benötigt. JRE muss von
der Sun-Webseite heruntergeladen werden.
Daisysim2.ZIP (47,7K)
- Der Inhalt dieser Webseite:
Das Zip-file enthält eine Postscript-Datei im Booklet-Format, die unter Latex erstellt wurde und wie üblich mit GhostView
angeschaut und gedruckt werden kann.
Daisyweb.ZIP (245K)
Rolf Carstensen - 31.August 2001


 1 Worum geht es?
1 Worum geht es?




